Tổng Quan
Bài viết minh họa phân tích cấu trúc tự động của tiết diện dầm bê tông sử dụng gói Python mã nguồn mở sectionproperties.
Phân tích bao gồm:
- Định Nghĩa Vật Liệu: Bê tông với các tính chất đàn hồi
- Tạo Hình Học: Tiết diện dầm được định nghĩa theo chương trình (thay thế nhập DXF)
- Tạo Lưới: Tạo lưới phần tử hữu hạn
- Tính Toán Tính Chất: Tính chất hình học, uốn và dẻo
- Phân Tích Độ Cứng: Độ cứng trục, uốn và xoắn
- Phân Tích Ứng Suất: Nhiều trường hợp tải với trực quan hóa
- Vòng Mohr: Trực quan hóa trạng thái ứng suất tới hạn
Tiết Diện Thiết Kế
Tiết Diện dầm Bê Tông
- Vật liệu: Bê tông (E = 30,1 GPa, ν = 0,2)
- Kích thước lưới: 60 mm²
- Tải Áp Dụng:
- Lực dọc trục: 10 kN
- Mô-men Uốn (M_xx): 10 kN·m
- Lực cắt theo phương x (V_x): 25 kN
- Lực cắt theo phương y (V_y): 50 kN
1. Nhập Các Thư Viện Cần Thiết
Nhập tất cả các thư viện cần thiết để tạo hình học, tạo lưới và phân tích phần tử hữu hạn.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
from shapely.geometry import Polygon
# Nhập các mô-đun sectionproperties cho tạo hình học và định nghĩa vật liệu
from sectionproperties.pre.geometry import Geometry
from sectionproperties.pre.pre import Material
# In thông báo xác nhận các thư viện đã được nhập thành công
print("Thư viện được nhập thành công")
print(f"Phiên bản NumPy: {np.__version__}")
print(f"Phiên bản Matplotlib: {plt.matplotlib.__version__}")
2. Định Nghĩa Tính Chất Vật Liệu
Tạo vật liệu Bê tông với các tính chất đàn hồi, cơ học và vật lý được chỉ định theo thông số kỹ thuật.
# Định nghĩa các tính chất vật liệu cho bê tông (theo thông số kỹ thuật của nhiệm vụ)
concrete_properties = {
"name": "Bê Tông",
"elastic_modulus": 30.1e3, # MPa - Mô-đun đàn hồi (Young's modulus)
"poissons_ratio": 0.2, # Tỷ lệ Poisson - độ co ngót
"density": 2.4e-6, # kg/mm³ - Mật độ của bê tông
"yield_strength": 32, # MPa - Sức chịu nén của bê tông
"color": "lightgrey" # Màu sắc để vẽ trên biểu đồ
}
# Tạo đối tượng Material sectionproperties với các tính chất vật liệu định nghĩa ở trên
concrete = Material(
name=concrete_properties["name"],
elastic_modulus=concrete_properties["elastic_modulus"],
poissons_ratio=concrete_properties["poissons_ratio"],
density=concrete_properties["density"],
yield_strength=concrete_properties["yield_strength"],
color=concrete_properties["color"]
)
# In bảng tóm tắt các tính chất vật liệu để xác minh
print("\n" + "="*70)
print("TÍNH CHẤT VẬT LIỆU - BÊ TÔNG")
print("="*70)
print(f"Tên: {concrete_properties['name']}")
print(f"Mô-đun Đàn Hồi (E): {concrete_properties['elastic_modulus']:,.1f} MPa")
print(f"Tỷ Lệ Poisson (ν): {concrete_properties['poissons_ratio']:.2f}")
print(f"Mật Độ (ρ): {concrete_properties['density']:.2e} kg/mm³")
print(f"Sức Chịu Nén (f_y): {concrete_properties['yield_strength']:,.1f} MPa")
print(f"Màu: {concrete_properties['color']}")
3. Xây Dựng Hình Học Tiết Diện dầm
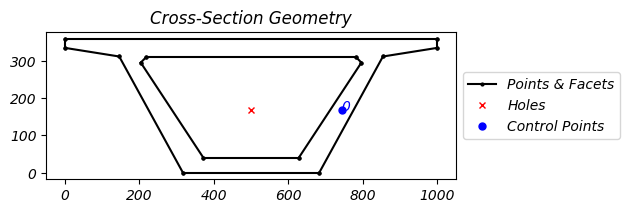
Tải hình học tiết diện dầm từ tệp DXF. Hình học tiết diện dầm bê tông cầu điển hình với các đặc trưng sau:
- Mặt trên rộng để chịu tải
- Lõi trung tâm rỗng để giảm khối lượng
- Các góc bo tròn cho sự mượt mà
- Các bức tường bên dày để chịu lực cắt
try:
# Tải hình học từ tệp DXF
geom = Geometry.from_dxf(dxf_filepath="./dxf/box-girder.dxf")
# Gán vật liệu bê tông cho hình học
geom.material = concrete
# Vẽ hình học trên màn hình
geom.plot_geometry()
print("Hình học được tải từ tệp DXF thành công")
except Exception as e:
# Nếu tệp DXF không tìm thấy, in thông báo lỗi
print(f"Không thể tải tệp DXF: {e}")
print("Sử dụng hình học được xác định lập trình...")
Mặt cắt ngang dầm:
4. Tạo Lưới Phần Tử Hữu Hạn
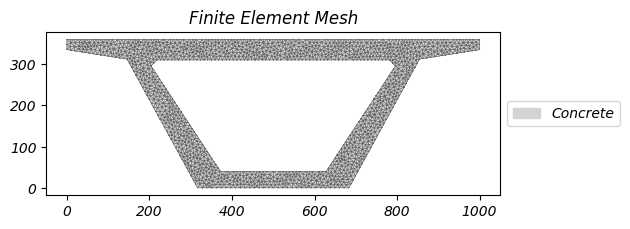
Lưới hóa (meshing) là một bước cực kỳ quan trọng trong phân tích phần tử hữu hạn (FEA). Nó chia nhỏ hình học phức tạp thành các phần tử đơn giản mà máy tính có thể xử lý. Lưới trực tiếp ảnh hưởng đến:
- Độ chính xác: Lưới mịn cho kết quả chính xác hơn
- Độ tin cậy: Lưới kém có thể cho kết quả sai
- Thời gian tính toán: Lưới mịn tăng thời gian xử lý
Cân bằng mật độ lưới là chìa khóa để tối ưu hóa: lưới mịn trong các vùng quan trọng nhưng lưới thô ở các vùng ít quan trọng.
# Nhập module Section từ sectionproperties.analysis để thực hiện FEA
from sectionproperties.analysis import Section
# Tạo lưới với kích thước phần tử 60 mm² (tối ưu cho độ chính xác và tốc độ)
geom.create_mesh(mesh_sizes=60)
# Tạo đối tượng Section cho phân tích phần tử hữu hạn
sec = Section(geom)
# Hiển thị lưới trên màn hình để kiểm tra chất lượng
sec.plot_mesh()
plt.show()
Lưới phần tử hữu hạn mặt cắt ngang dầm:
5. Tính Toán Các Tính Chất Hình Học
Sau khi tạo lưới phần tử, chúng ta có thể tính toán các tính chất hình học quan trọng của tiết diện, bao gồm:
- Tính chất hình học: Diện tích, tâm, mô-men quán tính
- Tính chất uốn: Hằng số uốn và tính chất liên quan
- Tính chất dẻo: Mô-men dẻo và vị trí tâm dẻo
# Tính toán tính chất hình học của tiết diện (diện tích, tâm, mô-men quán tính)
sec.calculate_geometric_properties()
# Tính toán tính chất uốn của tiết diện (deplanation, bimoment, torsion constant)
sec.calculate_warping_properties()
# Tính toán tính chất dẻo của tiết diện (plastic section modulus, plastic centroid)
sec.calculate_plastic_properties()
# Hiển thị tất cả kết quả tính toán với định dạng 2 chữ số thập phân
sec.display_results(fmt=".2f")
6. Các Đặc trưng Độ Cứng
Độ cứng là một chỉ số quan trọng cho biết tiết diện sẽ chống lại biến dạng như thế nào. Chúng ta sẽ tính ba loại độ cứng chính:
- Độ cứng trục (EA): Chống lại lực kéo/nén
- Độ cứng uốn (EI): Chống lại mô-men uốn
- Độ cứng xoắn (GJ): Chống lại mô-men xoắn
# Tính độ cứng trục EA = E × A (chống lại lực kéo/nén)
ea = sec.get_ea()
# Tính độ cứng uốn EI = E × I (chống lại mô-men uốn) - chỉ lấy Ixx (quanh trục x)
eixx, _, _ = sec.get_eic()
# Tính hằng số uốn EJ = E × J (liên quan đến uốn)
ej = sec.get_ej()
# Tính độ cứng xoắn GJ = G × J (chống lại mô-men xoắn)
gj = sec.get_g_eff() / sec.get_e_eff() * ej
# In các kết quả độ cứng ở dạng ký hiệu khoa học
print(f"Độ cứng trục (E.A): {ea:.3e} N")
print(f"Độ cứng uốn (E.I): {eixx:.3e} N.mm2")
print(f"Độ cứng xoắn (G.J): {gj:.3e} N.mm2")
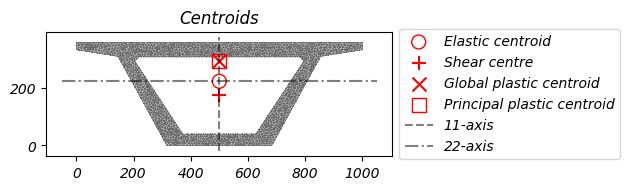
7. Trực Quan Hóa Các Tâm Hình Học
Ngoài các tính chất cơ bản, chúng ta có thể trực quan hóa các tâm đặc biệt của tiết diện để hiểu rõ hơn về phân bố hình học:
- Tâm đàn hồi: Điểm tương tức tải trọng trục gây uốn
- Tâm cắt: Điểm tương ứng tác dụng lực cắt để không gây xoắn
- Tâm dẻo: Điểm tương ứng với chuyển động dẻo
- Trục chính: Hướng của các mô-men quán tính chính
# Vẽ tất cả các tâm hình học quan trọng: tâm đàn hồi, tâm cắt, tâm dẻo, và trục chính
sec.plot_centroids()
Hiển thị trọng tâm hình học của mặt cắt:
8. Phân Tích Ứng Suất
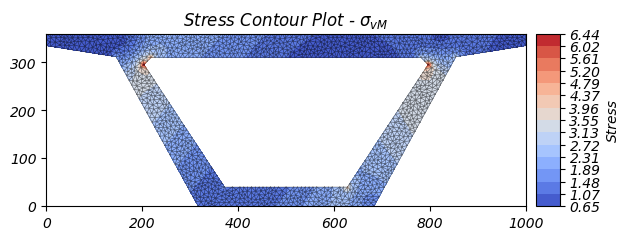
Cuối cùng, chúng ta sẽ tính toán và trực quan hóa các ứng suất trong tiết diện. Giả sử tiết diện này thuộc nhịp trung tâm của một dầm đơn giản được gối tựa hai đầu. Dầm chịu một sự kết hợp các tải bên ngoài:
- N = 10 kN: Tải trục (kéo hoặc nén)
- M_xx = 10 kN·m: Mô-men uốn quanh trục x (gây cong dầm)
- V_x = 25 kN: Lực cắt theo hướng x
- V_y = 50 kN: Lực cắt theo hướng y
Ứng Suất Von Mises
# Tính toán ứng suất trên toàn bộ tiết diện với các tải đã chỉ định
# N=10kN (tải trục), Mxx=10kNm (mô-men uốn), Vx=25kN, Vy=50kN (lực cắt)
stress = sec.calculate_stress(n=10e3, mxx=10e6, vx=25e3, vy=50e3)
# Vẽ ứng suất Von Mises (tổng ứng suất tương đương) trên toàn bộ tiết diện
# normalize=False: không chuẩn hóa, hiển thị giá trị thực tế
stress.plot_stress(stress="vm", normalize=False, fmt="{x:.2f}")
Biểu đồ ứng suất của mặt cắt Dầm:
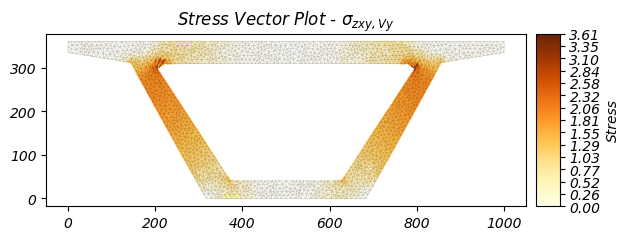
Trực Quan Hóa Vectơ Ứng Suất Cắt
Ngoài ứng suất Von Mises, chúng ta cũng có thể hiển thị các vectơ ứng suất cắt để thấy rõ hơn nơi và cách ứng suất cắt tập trung:
# Vẽ trường vectơ ứng suất cắt theo hướng y (Vy) và ứng suất cắt Zxy
# Các vectơ cho thấy hướng và độ lớn của ứng suất cắt tại mỗi điểm
stress.plot_stress_vector(stress="vy_zxy", fmt="{x:.2f}")
Biểu đồ Vectơ ứng suất cắt của mặt cắt Dầm:
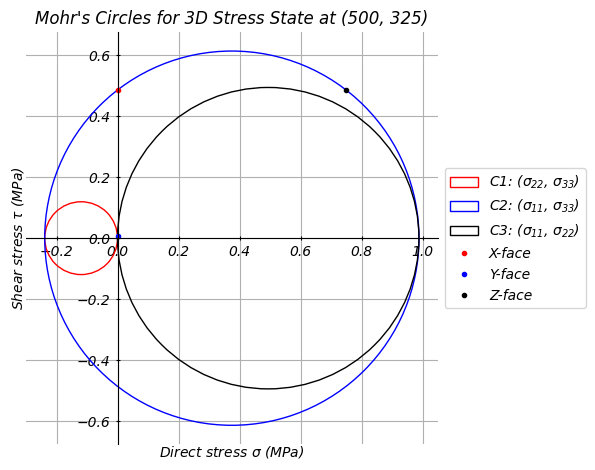
Vòng tròn Mohr Ứng suất
Vòng tròn Mohr là biểu đồ hình học giúp xác định ứng suất chính, ứng suất cắt cực đại, và trạng thái ứng suất tại một điểm cụ thể. Chúng ta sẽ vẽ Vòng Mohr tại điểm (x=500, y=325) - một điểm tới hạn trong tiết diện:
# Vẽ Vòng Mohr tại điểm cụ thể (500, 325) mm để xác định ứng suất chính
# Điểm này được chọn vì gần ranh giới của tiết diện nơi ứng suất thường cao
stress.plot_mohrs_circles(x=500, y=325)
# Hiển thị tất cả các biểu đồ
plt.show()
Biểu đồ Vòng tròn Mohr ứng suất:
9. Tóm Tắt và Kết Luận
Phân tích này kiểm tra chi tiết tiết diện dầm bê tông cầu trong các điều kiện tải kết hợp phức tạp bằng cách sử dụng các nguyên tắc phân tích phần tử hữu hạn (FEA). Các kết quả chính được tóm tắt dưới đây:
Hình Học Tiết Diện:
- Tải từ tệp DXF (nếu khả dụng) hoặc được tạo lập trình
- Tiết diện dầm hình chữ nhật rỗng - tối ưu chi phí
- Các góc bo tròn - giảm tập trung ứng suất
- Bề dày tường bên - chịu lực cắt và uốn
Tính Chất Vật Liệu Bê Tông:
- Mô-đun Đàn Hồi (E): 30,1 kGPa = 30.100 MPa
- Tỷ Lệ Poisson (ν): 0,2 - độ co ngót của vật liệu
- Sức Chịu Nén: 32 MPa - sức chịu đựng tối đa
- Trọng lượng riêng: 2,4e-6 kg/mm³ - khối lượng trên đơn vị thể tích
Tính Chất Tiết Diện Tính Toán:
- Diện tích mặt cắt ngang (A) - chống lại tải trục
- Vị trí tâm (Cx, Cy) - điểm trọng tâm hình học
- Mô-men quán tính (Ixx, Iyy, Ixy) - chống lại uốn
- Hằng số uốn (J) - chống lại xoắn
Các Trường Hợp Tải Áp Dụng:
- Lực Trục: N = 10 kN
- Mô-men Uốn (quanh trục x): M_xx = 10 kN·m
- Lực Cắt theo x: V_x = 25 kN
- Lực Cắt theo y: V_y = 50 kN
Phân tích hoàn chỉnh tạo ra các kết quả sau:
- Trực Quan Hóa Hình Học: Xác nhận hình học tiết diện dầm rỗng với các thành phần chính
- Lưới Phần Tử Hữu Hạn: Chia tiết diện thành các phần tử 60 mm² để tinh chỉnh đầy đủ
- Ma Trận Độ Cứng: Tính toán độ cứng trục (EA), uốn (EI), và xoắn (GJ)
- Phân Bố Ứng Suất Von Mises: Hiển thị vùng chịu ứng suất cao trên toàn bộ tiết diện
- Trường Vectơ Ứng Suất Cắt: Cho thấy mô hình tập trung ứng suất cắt
- Phân Tích Tâm Hình Học: Xác định vị trí các tâm đàn hồi, dẻo, cắt và trục chính
- Vòng tròn Mohr Ứng suất: Xác định ứng suất chính tại điểm tới hạn (500, 325)