Quy hoạch tuyến tính (Linear Programming - LP) là một trong những kỹ thuật tối ưu hóa quan trọng nhất trong toán học ứng dụng và kinh tế. Bài viết này sẽ giới thiệu về cơ sở toán học của LP và cách triển khai giải quyết 3 bài toán thực tế bằng thư viện SciPy trong Python.
1. Cơ sở Toán học (Mathematical Foundations)
1.1. Định nghĩa bài toán
Quy hoạch tuyến tính là phương pháp tối ưu hóa một hàm mục tiêu tuyến tính, thỏa mãn các ràng buộc đẳng thức hoặc bất đẳng thức tuyến tính.
Mô hình toán học tổng quát:
\[\begin{aligned} & \text{Maximize} & & \mathbf{c}^\mathrm{T} \mathbf{x} \\ & \text{Subject to} & & A \mathbf{x} \leq \mathbf{b} \\ & & & \mathbf{x} \geq 0 \end{aligned}\]Trong đó:
- \(\mathbf{x}\) : Vector biến quyết định (variables).
- \(\mathbf{c}\) : Vector hệ số hàm mục tiêu (objective coefficients).
- \(A\) : Ma trận hệ số ràng buộc (constraint matrix).
- \(\mathbf{b}\) : Vector giới hạn (bounds).
1.2. Các Phương pháp giải chính
- Simplex Method (Đơn hình): Phát triển bởi George Dantzig (1947). Giải thuật di chuyển dọc theo các cạnh của đa diện khả thi để tìm cực trị tại các đỉnh.
- Interior Point Method (Điểm trong): Tiếp cận nghiệm tối ưu bằng cách di chuyển qua phần bên trong của vùng khả thi.
- Branch and Bound (Nhánh và Cận): Sử dụng cho quy hoạch nguyên (MILP) khi các biến phải là số nguyên.
2. Mô hình hóa 3 Bài toán Thực tế
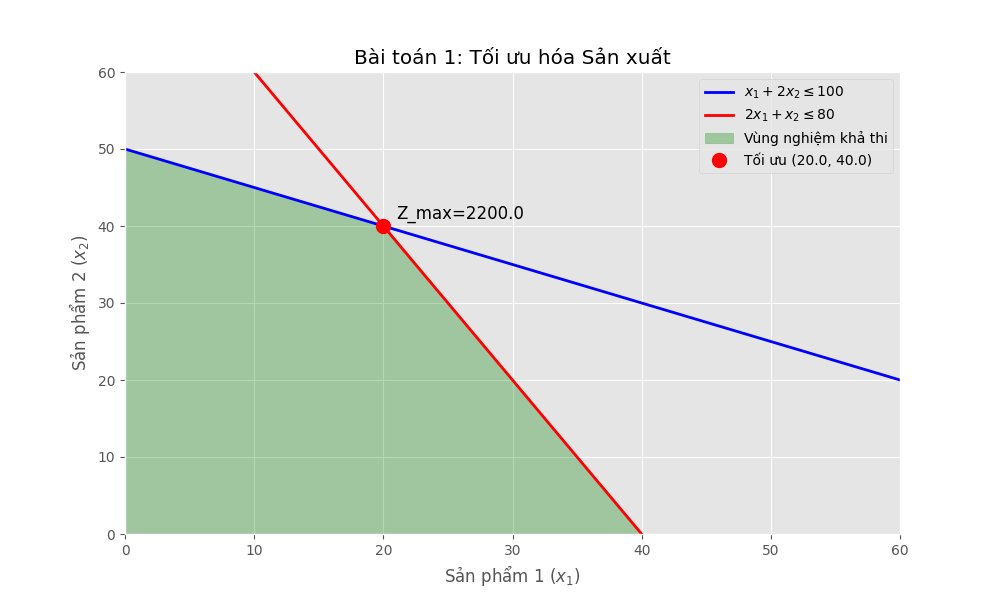
Bài toán 1: Quản lý Sản xuất (Production Mix)
Mục tiêu: Tối đa hóa lợi nhuận từ việc sản xuất 2 loại sản phẩm \(P_1, P_2\).
- Hàm mục tiêu: \(\text{Max } Z = 30x_1 + 40x_2\)
- Ràng buộc nguyên liệu: \(1x_1 + 2x_2 \leq 100\)
- Ràng buộc nhân công: \(2x_1 + 1x_2 \leq 80\)
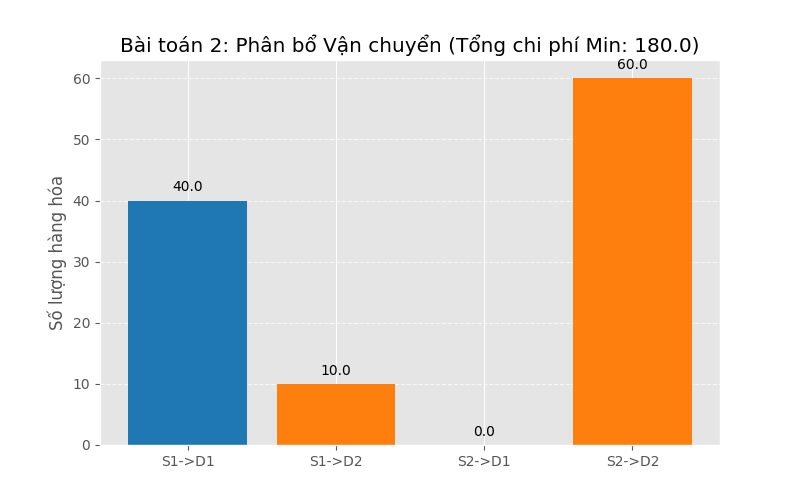
Bài toán 2: Vận chuyển (Transportation Problem)
Mục tiêu: Tối thiểu hóa chi phí vận chuyển từ 2 kho (S1, S2) đến 2 cửa hàng (D1, D2).
- Cung (Supply): \(S_1=50, S_2=60\)
- Cầu (Demand): \(D_1=40, D_2=70\)
- Hàm mục tiêu: \(\text{Min } Z = 2x_{11} + 4x_{12} + 3x_{21} + 1x_{22}\)
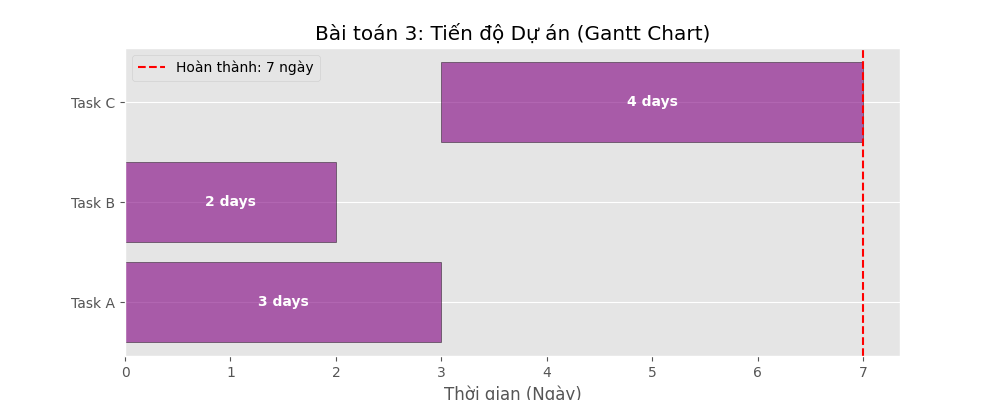
Bài toán 3: Quản lý Dự án (Project Management / CPM)
Mục tiêu: Tối thiểu hóa thời gian hoàn thành dự án gồm 3 công việc A, B, C.
- A (3 ngày), B (2 ngày) làm song song; C (4 ngày) làm sau A và B.
- Hàm mục tiêu: \(\text{Min } T_{end}\)
3. Triển khai với Python (SciPy)
Để giải quyết các bài toán này, chúng ta sử dụng thư viện scipy.optimize.linprog.
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import linprog
# Cấu hình hiển thị
plt.style.use('ggplot')
🛠 Giải Bài toán 1: Tối ưu hóa Sản xuất
# SciPy tìm Min, nên đảo dấu để tìm Max: Max(Z) <=> Min(-Z)
c_prod = [-30, -40]
A_prod = [[1, 2], [2, 1]]
b_prod = [100, 80]
res_prod = linprog(c_prod, A_ub=A_prod, b_ub=b_prod, bounds=(0, None), method='highs')
print(f"Lợi nhuận tối đa: {-res_prod.fun:.2f}")
print(f"Sản lượng x1: {res_prod.x[0]:.2f}, x2: {res_prod.x[1]:.2f}")
Kết quả trực quan hóa vùng nghiệm:
🚚 Giải Bài toán 2: Vận chuyển hàng hóa
# Hệ số chi phí: [x11, x12, x21, x22]
c_trans = [2, 4, 3, 1]
# Ràng buộc đẳng thức (Supply & Demand)
A_eq_trans = [
[1, 1, 0, 0], # Supply S1
[0, 0, 1, 1], # Supply S2
[1, 0, 1, 0], # Demand D1
[0, 1, 0, 1] # Demand D2
]
b_eq_trans = [50, 60, 40, 70]
res_trans = linprog(c_trans, A_eq=A_eq_trans, b_eq=b_eq_trans, bounds=(0, None), method='highs')
print(f"Chi phí tối thiểu: {res_trans.fun:.2f}")
print(f"Phân bổ: {res_trans.x}")
Biểu đồ phân phối hàng hóa:
📅 Giải Bài toán 3: Tiến độ Dự án (CPM)
# Biến: [t_A, t_B, t_C, t_End]. Mục tiêu: Min t_End
c_proj = [0, 0, 0, 1]
d_A, d_B, d_C = 3, 2, 4
# Ràng buộc thứ tự công việc
A_ub_proj = [
[1, 0, -1, 0], # t_A - t_C <= -3
[0, 1, -1, 0], # t_B - t_C <= -2
[0, 0, 1, -1] # t_C - t_End <= -4
]
b_ub_proj = [-d_A, -d_B, -d_C]
res_proj = linprog(c_proj, A_ub=A_ub_proj, b_ub=b_ub_proj, bounds=(0, None), method='highs')
print(f"Thời gian hoàn thành: {res_proj.fun:.1f} ngày")
Sơ đồ Gantt kết quả:
4. Kết luận
Quy hoạch tuyến tính là công cụ cực kỳ mạnh mẽ trong việc ra quyết định. Với sự hỗ trợ của các thư viện như SciPy, việc mô hình hóa và giải quyết các bài toán tối ưu hóa phức tạp trở nên dễ dàng và hiệu quả hơn bao giờ hết.
Nguồn tham khảo:
- Dantzig, G. B. (1963). Linear Programming and Extensions.
- SciPy Documentation:
scipy.optimize.linprog.
Cập nhật cuối: 2026-01-23