Markov Chain Monte Carlo (MCMC) is a powerful class of algorithms for sampling from probability distributions. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution to approximate complex integrals or understand posterior distributions in Bayesian statistics.
Markov Chain Monte Carlo (MCMC) là một lớp các thuật toán lấy mẫu từ phân phối xác suất. Bằng cách xây dựng một chuỗi Markov có phân phối cân bằng (equilibrium distribution) mong muốn, ta có thể lấy mẫu từ phân phối đó để xấp xỉ các tích phân phức tạp hoặc hiểu rõ hơn về tính chất của phân phối hậu nghiệm (posterior) trong thống kê Bayes.
1. Markov Chain (Chuỗi Markov)
A Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.
Chuỗi Markov là một mô hình ngẫu nhiên mô tả một chuỗi các biến cố khả dĩ, trong đó xác suất của mỗi biến cố chỉ phụ thuộc vào trạng thái đạt được trong biến cố trước đó.
- Markov Property / Tính chất Markov: The future depends only on the present, not on the past.
Tương lai chỉ phụ thuộc vào hiện tại, không phụ thuộc vào quá khứ. \(P(X_{n+1} | X_n, X_{n-1}, ..., X_0) = P(X_{n+1} | X_n)\) - Transition Matrix / Ma trận chuyển trạng thái: Describes the probabilities of moving from one state to another.
Mô tả xác suất chuyển từ trạng thái này sang trạng thái khác. - Equilibrium / Trạng thái cân bằng: After a sufficiently large number of steps, the probability distribution of the states converges to a stable distribution.
Sau một số bước đủ lớn, phân phối xác suất của trạng thái hội tụ về một phân phối ổn định, không thay đổi qua các bước tiếp theo.
2. Monte Carlo Method (Phương pháp Monte Carlo)
Monte Carlo methods are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results.
Phương pháp Monte Carlo là một nhóm các thuật toán tính toán dựa vào việc lấy mẫu ngẫu nhiên lặp lại để thu được các kết quả số.
- Principle / Nguyên lý: Use randomness to solve problems that might be deterministic in principle.
Sử dụng tính ngẫu nhiên để giải quyết các bài toán có thể xác định (deterministic) về nguyên tắc. - Law of Large Numbers / Quy luật số lớn: As the number of samples increases, the sample mean converges to the true expected value.
Khi số lượng mẫu thử nghiệm tăng lên, kết quả trung bình của mẫu sẽ hội tụ về giá trị kỳ vọng thực sự.
3. Bayesian Inference (Suy luận Bayesian)
Bayesian inference is a method of statistical inference in which Bayes’ theorem is used to update the probability for a hypothesis as more evidence or information becomes available.
Suy luận Bayes là phương pháp thống kê trong đó xác suất được sử dụng để định lượng sự không chắc chắn. Định lý Bayes cập nhật xác suất cho một giả thuyết khi có thêm bằng chứng hoặc thông tin mới.
Where / Trong đó:
-
$P(\theta D)$: Posterior - Probability of parameter $\theta$ given data $D$. (Xác suất của tham số $\theta$ khi đã biết dữ liệu $D$.) -
$P(D \theta)$: Likelihood - Probability of observing data $D$ given parameter $\theta$. (Xác suất quan sát dữ liệu $D$ nếu tham số là $\theta$.) - $P(\theta)$: Prior - Initial belief about $\theta$ before seeing data. (Niềm tin ban đầu về $\theta$ trước khi thấy dữ liệu.)
- $P(D)$: Evidence - Normalizing constant. (Hằng số chuẩn hóa, thường rất khó tính toán trực tiếp trong không gian nhiều chiều.)
4. Markov Chain Monte Carlo (MCMC)
Why MCMC? / Tại sao cần MCMC?
In Bayesian statistics, calculating the posterior distribution $P(\theta | D)$ directly is often difficult because the denominator $P(D)$ requires integration over the entire parameter space.
Trong thống kê Bayes, việc tính toán trực tiếp phân phối hậu nghiệm $P(\theta | D)$ thường gặp khó khăn do mẫu số $P(D)$ đòi hỏi tích phân qua toàn bộ không gian tham số (vốn có thể có số chiều rất lớn).
MCMC solves this by sampling from the posterior distribution without calculating the normalizing constant $P(D)$.
MCMC giải quyết vấn đề này bằng cách lấy mẫu từ phân phối hậu nghiệm mà không cần tính hằng số chuẩn hóa $P(D)$.
How it works / Cách thức hoạt động
MCMC combines two methods:
MCMC kết hợp hai phương pháp:
- Monte Carlo: Random sampling to estimate the distribution. (Lấy mẫu ngẫu nhiên để ước lượng phân phối.)
- Markov Chain: Generating dependent samples such that the limiting distribution is the target distribution. (Tạo ra các mẫu phụ thuộc nhau sao cho phân phối giới hạn của chuỗi chính là phân phối mục tiêu.)
In other words, we design a “robot” that jumps randomly in the parameter space. The robot tends to stay longer in high-probability regions and visits low-probability regions less often.
Hay nói cách khác, ta thiết kế một “con robot” nhảy ngẫu nhiên trong không gian tham số. Con robot có xu hướng ở lại lâu hơn tại những vùng có xác suất cao và ít ghé thăm những vùng có xác suất thấp. Dấu vết bước chân của robot chính là các mẫu từ phân phối cần tìm.
Common Algorithms / Các thuật toán phổ biến
- Metropolis-Hastings (MH): General algorithm, proposes jumps and accepts/rejects based on probability density ratio.
Thuật toán tổng quát, đề xuất bước nhảy và chấp nhận/từ chối dựa trên tỷ lệ mật độ xác suất. - Gibbs Sampling: Special case of MH, updates one variable at a time while fixing others.
Trường hợp đặc biệt của MH, cập nhật từng biến một khi cố định các biến khác. - Hamiltonian Monte Carlo (HMC) / NUTS: Uses gradients to propose more efficient jumps (used in Stan, PyMC3).
Sử dụng đạo hàm (gradient) của hàm mật độ để đề xuất các bước nhảy hiệu quả hơn (Thường được dùng trong Stan, PyMC3). - Affine Invariant Ensemble Sampler (emcee): Uses multiple “walkers” in parallel, efficient for skewed distributions.
Sử dụng nhiều “walkers” song song, hiệu quả cho các phân phối méo mó.
5. Practical Applications / Ứng dụng thực tế
Civil Engineering & Project Management / Kỹ thuật Xây dựng & Quản lý Dự án
- Project Risk Analysis: Simulating project completion time (PERT/CPM) when task durations are random variables. MCMC estimates the probability of deadline overrun.
Phân tích rủi ro dự án: Mô phỏng thời gian hoàn thành dự án (PERT/CPM) khi thời gian từng tác vụ là biến ngẫu nhiên. MCMC giúp ước lượng phân phối xác suất của ngày hoàn thành. - Structural Reliability: Assessment of structural failure probability under random loads (wind, earthquake) and uncertain material properties.
Độ tin cậy kết cấu: Đánh giá xác suất phá hủy của kết cấu chịu tải trọng ngẫu nhiên (gió, động đất) và đặc trưng vật liệu không chắc chắn. - Design Optimization: Finding optimal design parameters in complex spaces.
Tối ưu hóa thiết kế: Tìm kiếm các tham số thiết kế tối ưu trong không gian phức tạp.
Finance, Economics & Investment / Tài chính, Kinh tế & Đầu tư
- Portfolio Optimization: Estimating profit and risk distribution (VaR - Value at Risk). MCMC allows modeling of non-normal fat-tailed return distributions.
Danh mục đầu tư: Ước lượng phân phối lợi nhuận và rủi ro (VaR). MCMC cho phép mô hình hóa các phân phối lợi nhuận đuôi dày (fat-tailed) phi chuẩn, thực tế hơn so với giả định phân phối chuẩn truyền thống. - Stochastic Volatility: Forecasting asset price volatility, options pricing.
Mô hình hóa biến động: Dự báo biến động giá tài sản, định giá quyền chọn. - Algorithmic Trading: Detecting regime switching to adjust automated trading strategies.
Giao dịch thuật toán: Phát hiện sự thay đổi chế độ thị trường (regime switching models) để điều chỉnh chiến lược giao dịch tự động.
6. Simulation Summary (Tóm tắt tính toán Mô phỏng)
This section summarizes a simple Metropolis-Hastings implementation to fit a linear model ($y = mx + c$) to noisy data.
Phần này tóm tắt quá trình thực hiện thuật toán Metropolis-Hastings đơn giản để khớp mô hình đường thẳng ($y = mx + c$) vào dữ liệu nhiễu.
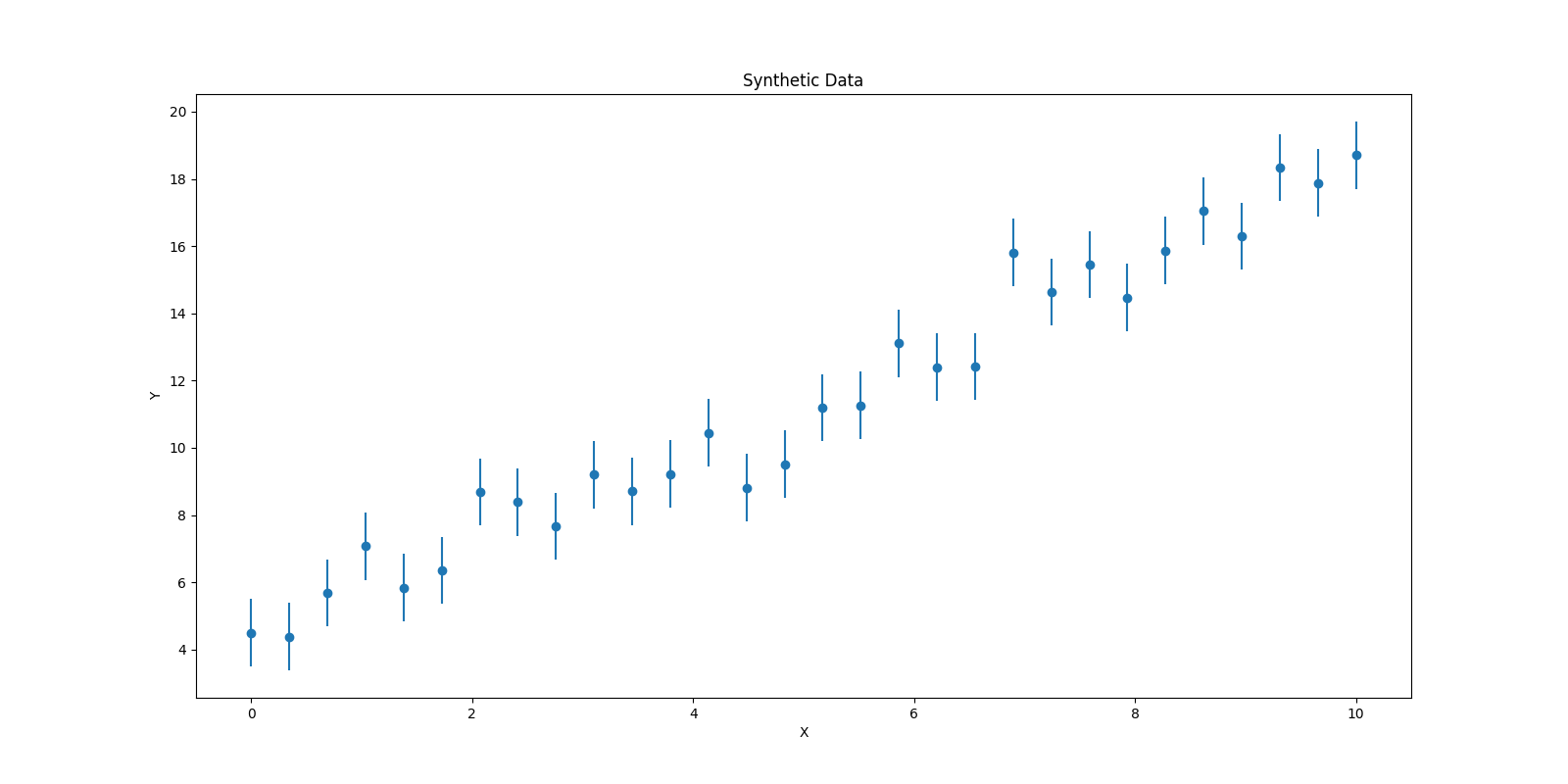
6.1. Synthetic Data / Dữ liệu giả định
Data generated with 30 points and error bars representing measurement uncertainty ($\sigma=1$).
Dữ liệu được tạo ra với 30 điểm. Các thanh sai số thể hiện độ không đảm bảo đo ($\sigma=1$).
6.2. Chains / Quá trình chạy chuỗi
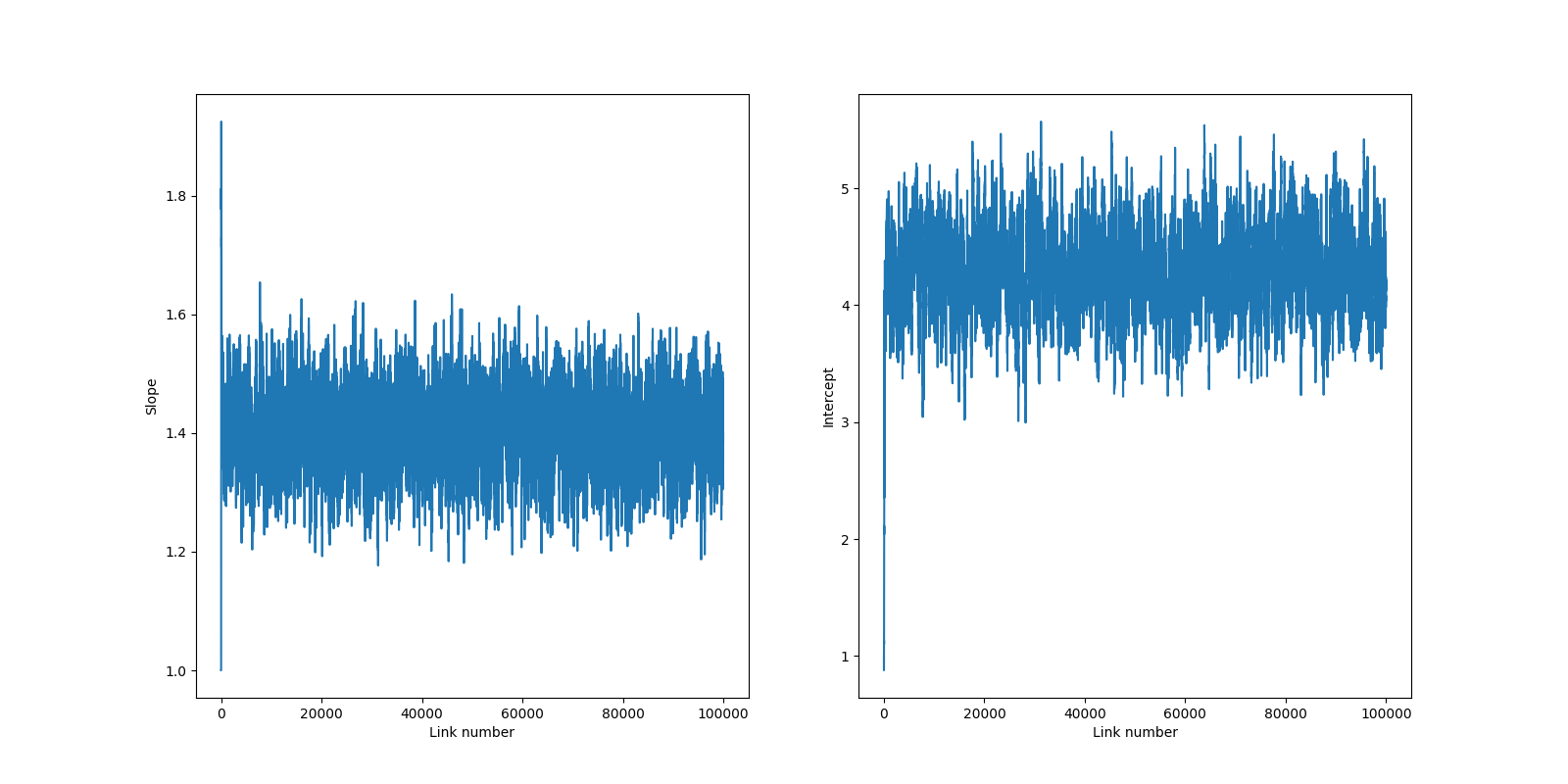
The algorithm typically runs for 100,000 steps. The trace plot shows the value of Slope and Intercept over iterations.
Thuật toán chạy 100,000 bước. Biểu đồ Trace plot cho thấy giá trị của Slope và Intercept qua các bước lặp.
6.3. Posterior Distributions / Phân phối Hậu nghiệm
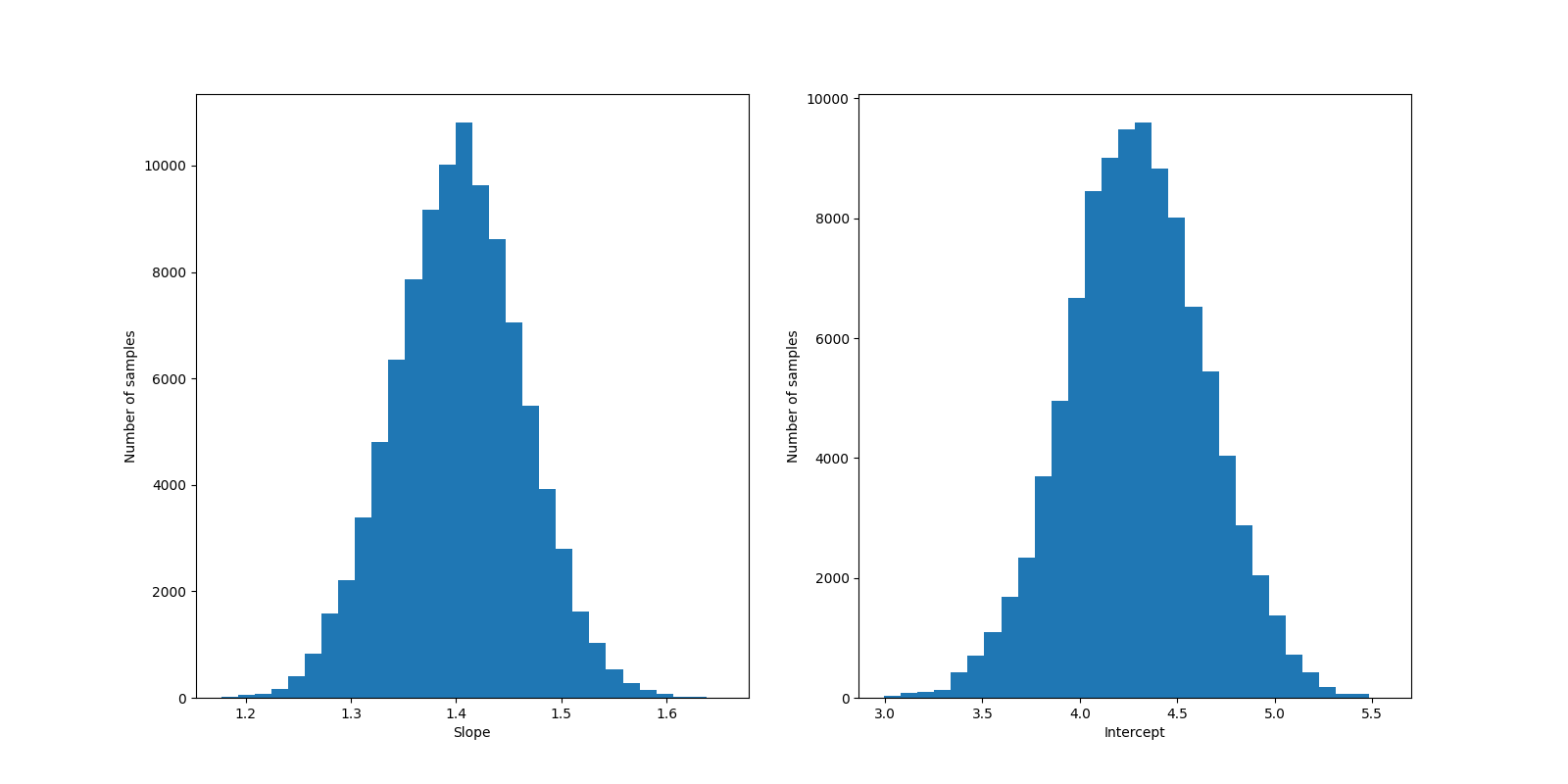
After removing the burn-in period, we obtain histograms of the parameters.
Sau khi loại bỏ giai đoạn đầu (burn-in), ta thu được phân phối tần suất (Histogram) của các tham số.
- Estimated Results / Kết quả ước lượng:
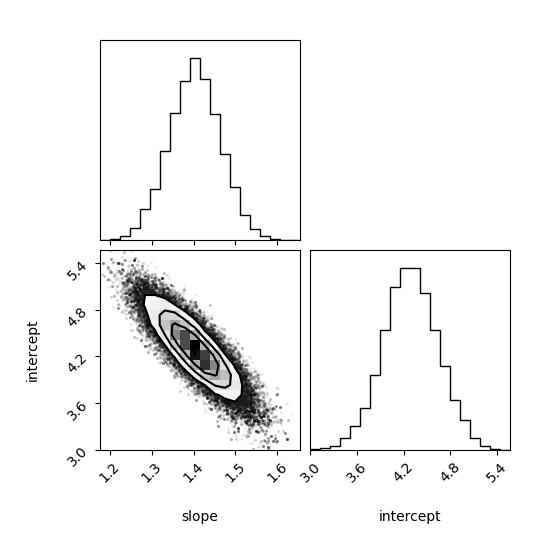
- Slope: ~1.40 (True: 1.5)
- Intercept: ~4.29 (True: 4.0)
6.4. Correlation / Tương quan tham số
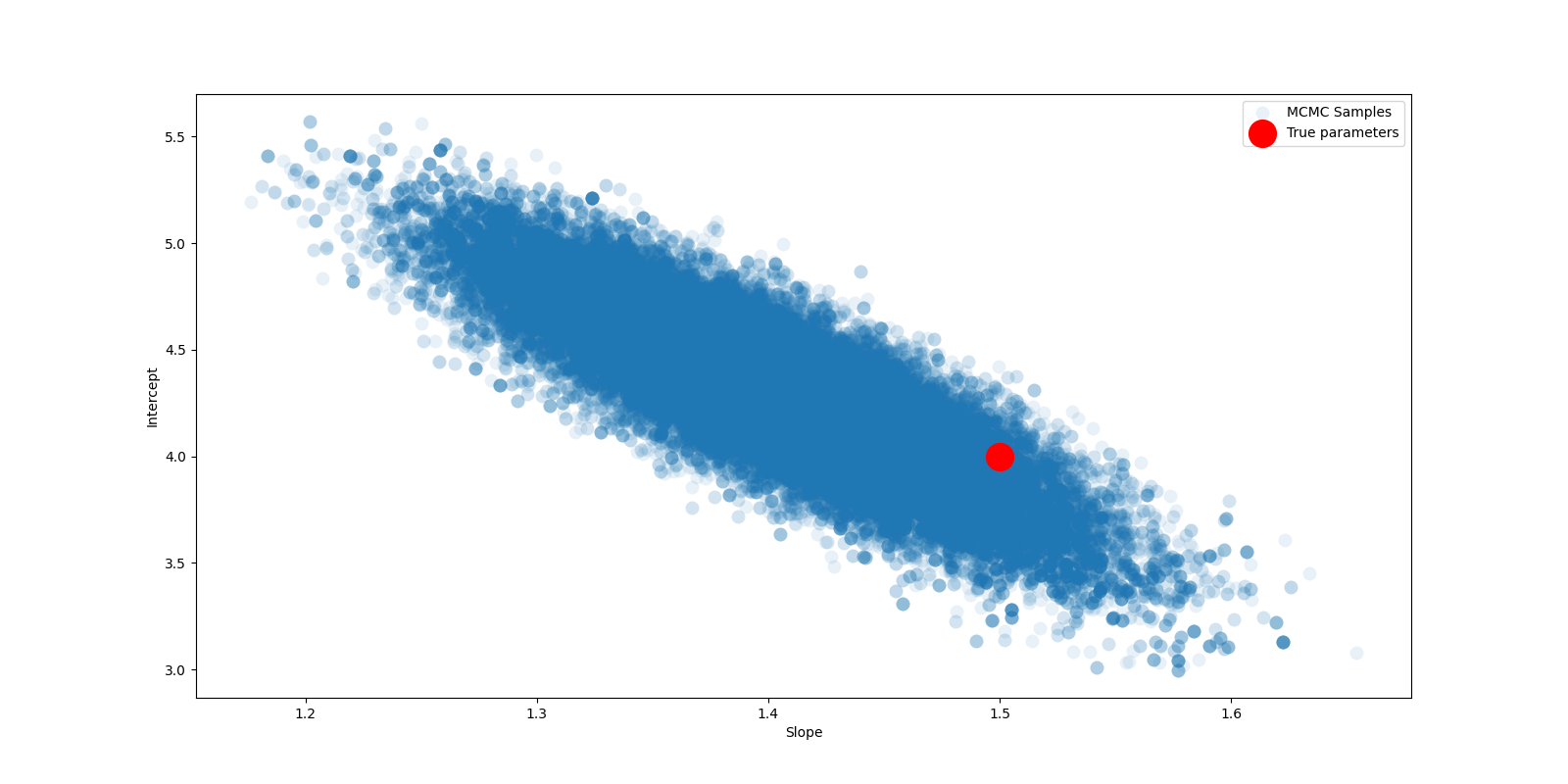
Scatter plot showing dependence between Slope and Intercept. Negative correlation is observed.
Biểu đồ phân tán cho thấy sự phụ thuộc giữa Slope và Intercept. Có sự tương quan âm: khi độ dốc tăng, hệ số chặn có xu hướng giảm.
6.5. Corner Plot
Corner plot showing marginal distributions on the diagonal and joint distributions off-diagonal.
Biểu đồ “Corner” thể hiện đồng thời phân phối biên trên đường chéo và phân phối đồng thời ngoài đường chéo.
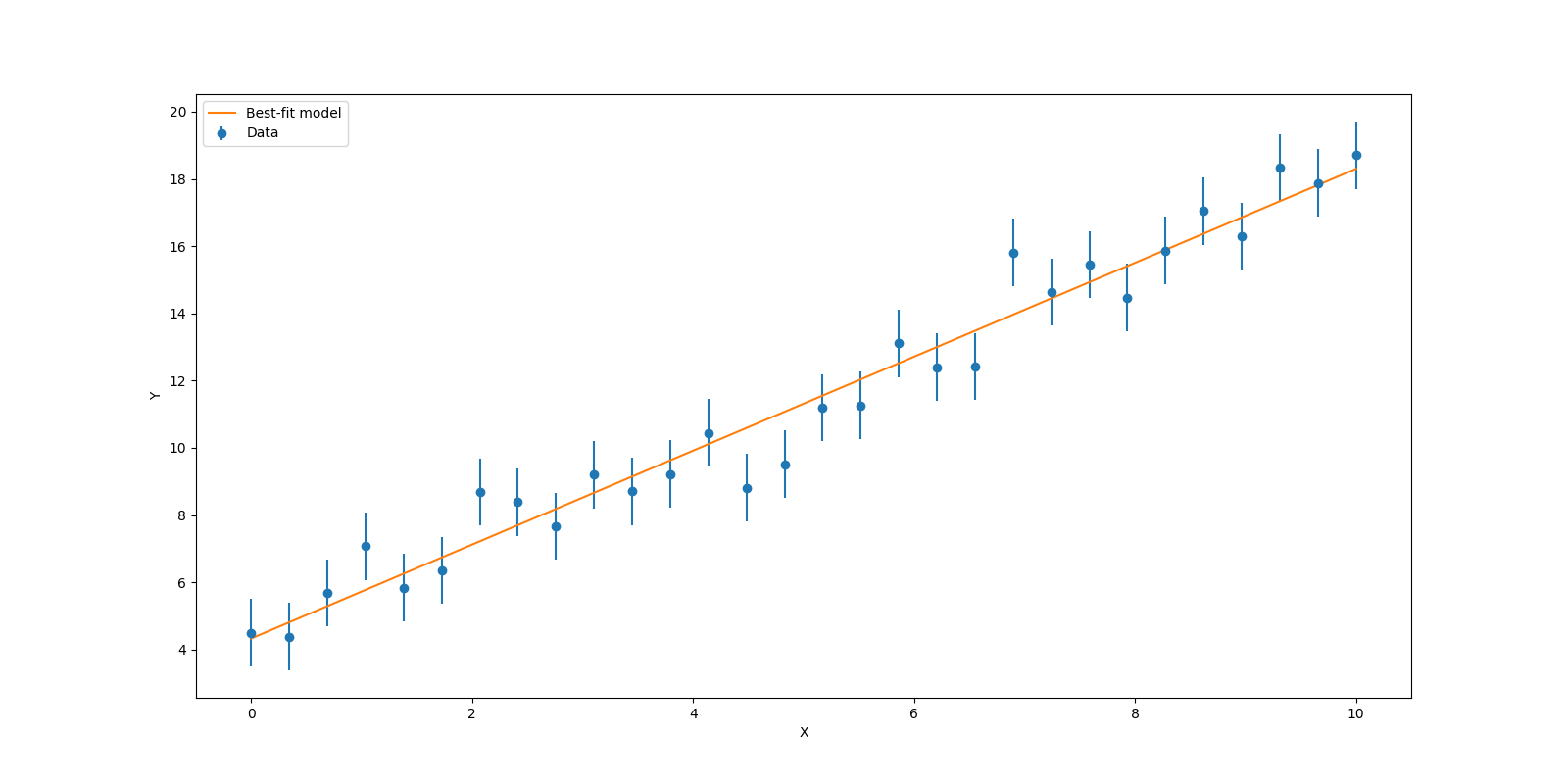
6.6. Best Fit / Kết quả Khớp mô hình
The line with the highest Likelihood is plotted over the data.
Đường thẳng từ bộ tham số có Likelihood cao nhất được vẽ chồng lên dữ liệu.
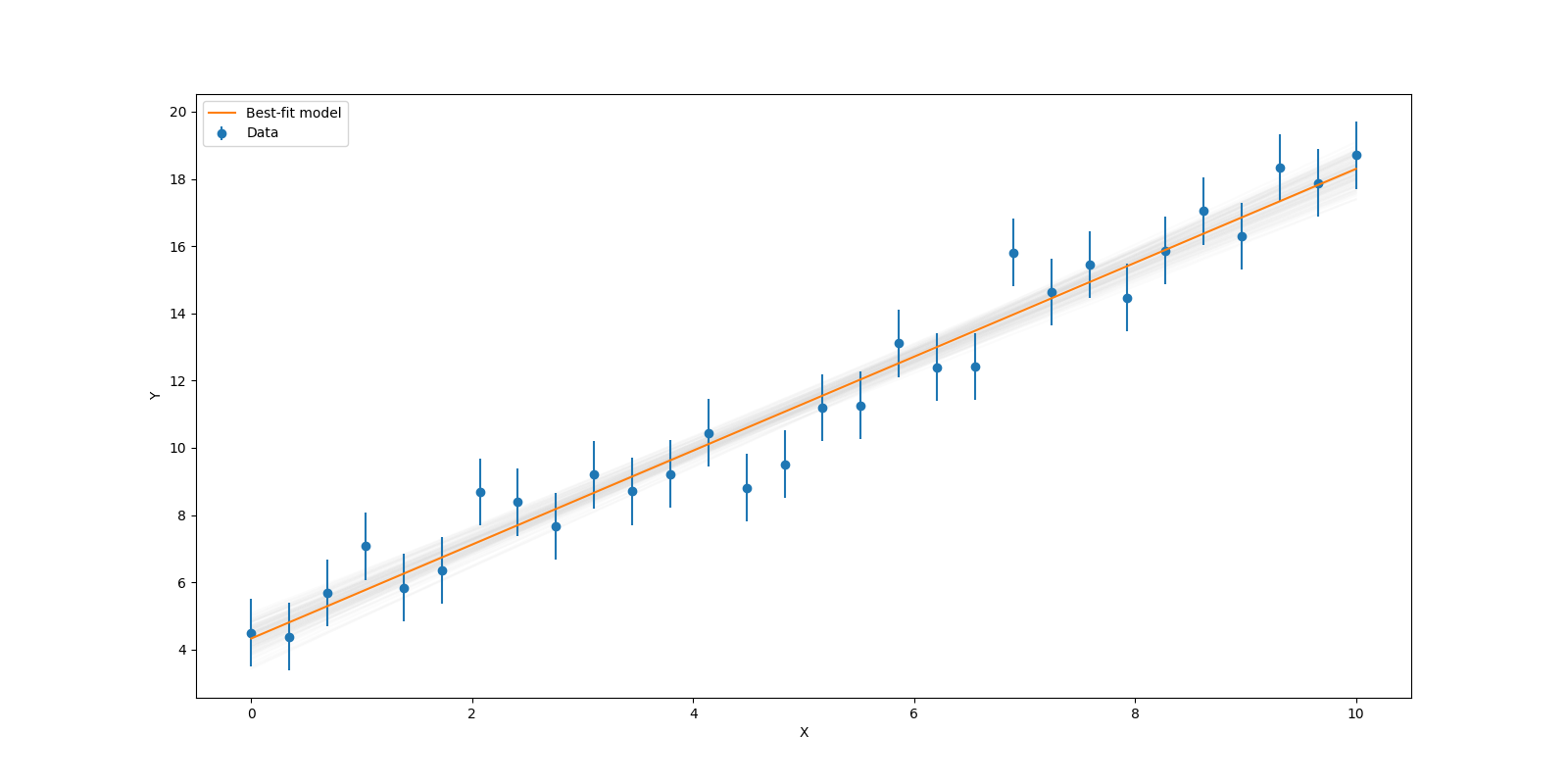
6.7. Model Uncertainty / Độ không đảm bảo của mô hình
Visualizing a sample of lines from the MCMC chain reveals the model uncertainty.
Bằng cách vẽ ngẫu nhiên 100 đường thẳng từ chuỗi MCMC, ta hình dung được độ không chắc chắn của mô hình.
References / Tài liệu tham khảo
- Wikipedia - Markov chain Monte Carlo: https://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo
- Stanford CS109 - Mathematical Foundations: https://web.stanford.edu/class/archive/cs/cs109/cs109.1218/files/student_drive/9.6.pdf